Operational Reconstruction of Quantum Formalism
Understanding the Foundations of Quantum Mechanics through Information-Theoretic Principles
Quantum Particle Statistics: Beyond Bosons and Fermions
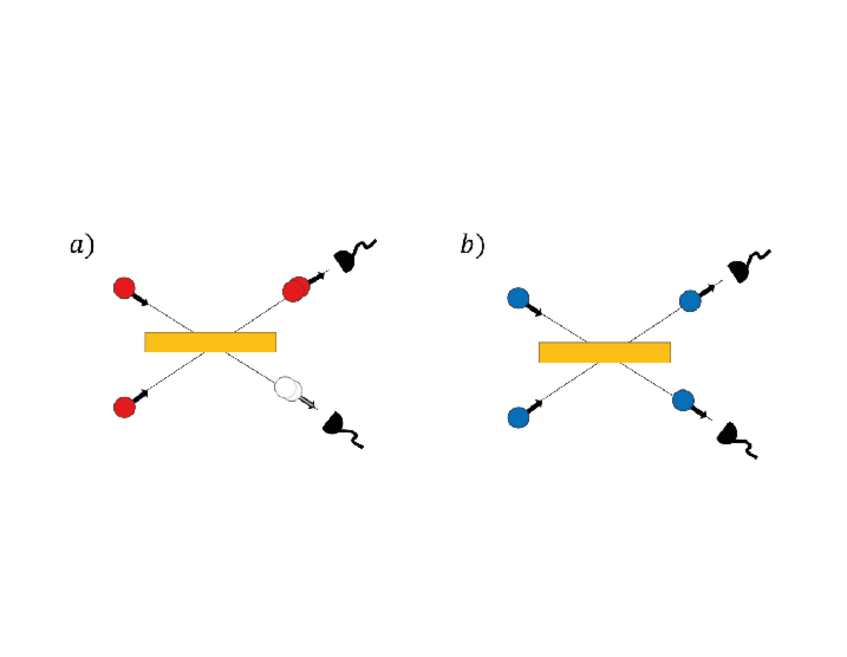
Quantum Particle Statistics: Beyond Bosons and Fermions
In quantum theory, identical particles are classified as bosons or fermions, a dichotomy rooted in the symmetrization postulate or commutation relations among creation and annihilation operators. Yet, the physical justification for this postulate remains elusive. Why are only these two types of statistics realized in Nature?
Our research reexamines this question through a quantum-information-theoretic framework. By starting from minimal operational assumptions—such as locality and reversibility of physical transformations—we recover bosonic and fermionic statistics as the only solutions consistent with the imposed structure. Intriguingly, the same framework also allows for a novel and consistent class of particle statistics, which we term transtatistics [OR1]. These generalized statistics differ conceptually and mathematically from known extensions like parastatistics, and may support intermediate computational models between boson sampling and fermionic computation.
Reconstructing Quantum Theory from First Principles
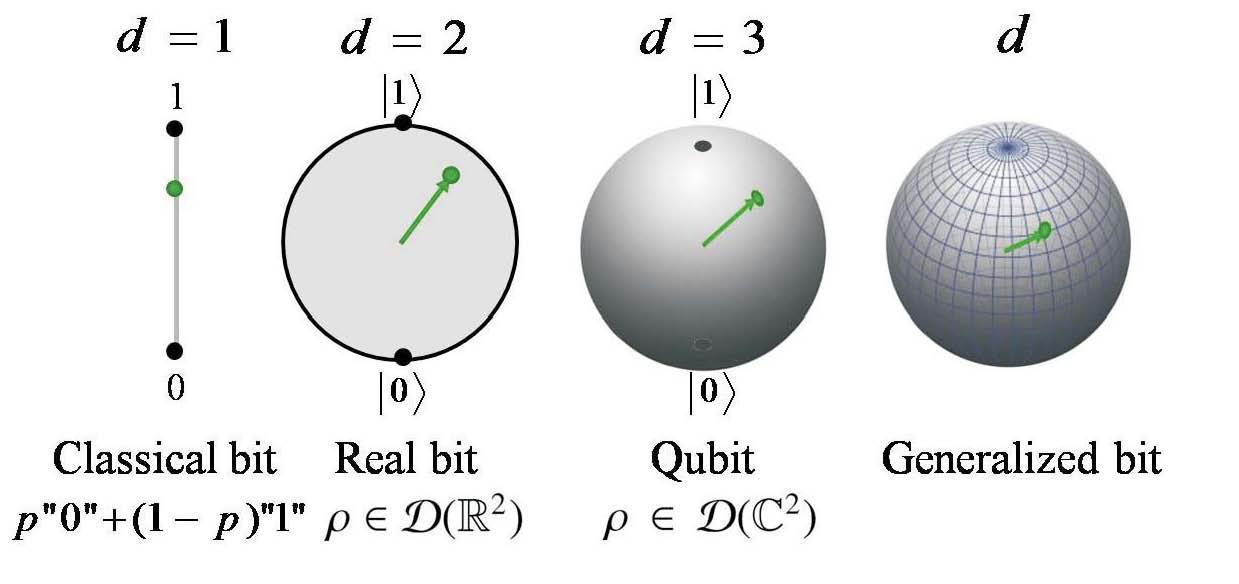
State spaces of a two-dimensional system in the generalized
probabilistic theories [DB09].
Reconstructing Quantum Theory from First Principles
A central aim of modern quantum foundations is to derive the formalism of quantum theory—its Hilbert space structure, state transformations, and measurement rules—from operationally meaningful postulates. This approach, known as reconstruction, shifts focus from mathematical axioms to physically motivated principles.
Following the pioneering work of Hardy [Har01], various reconstructions have identified quantum mechanics as uniquely compatible with a set of information-theoretic assumptions. In our work [DB09], we demonstrated that three simple principles are sufficient:
- Limited information capacity of elementary systems
- Continuous reversible dynamics
- Tomographic locality
These assumptions yield the full structure of finite-dimensional quantum theory, without recourse to ad hoc axioms like Hardy’s “simplicity.” A recurring theme in subsequent reconstructions is that quantum theory appears as the unique theory that combines reversibility with probabilistic indeterminism—in contrast to classical physics, which combines reversibility with determinism.
Quantum Theory and the Dimensionality of Physical Space
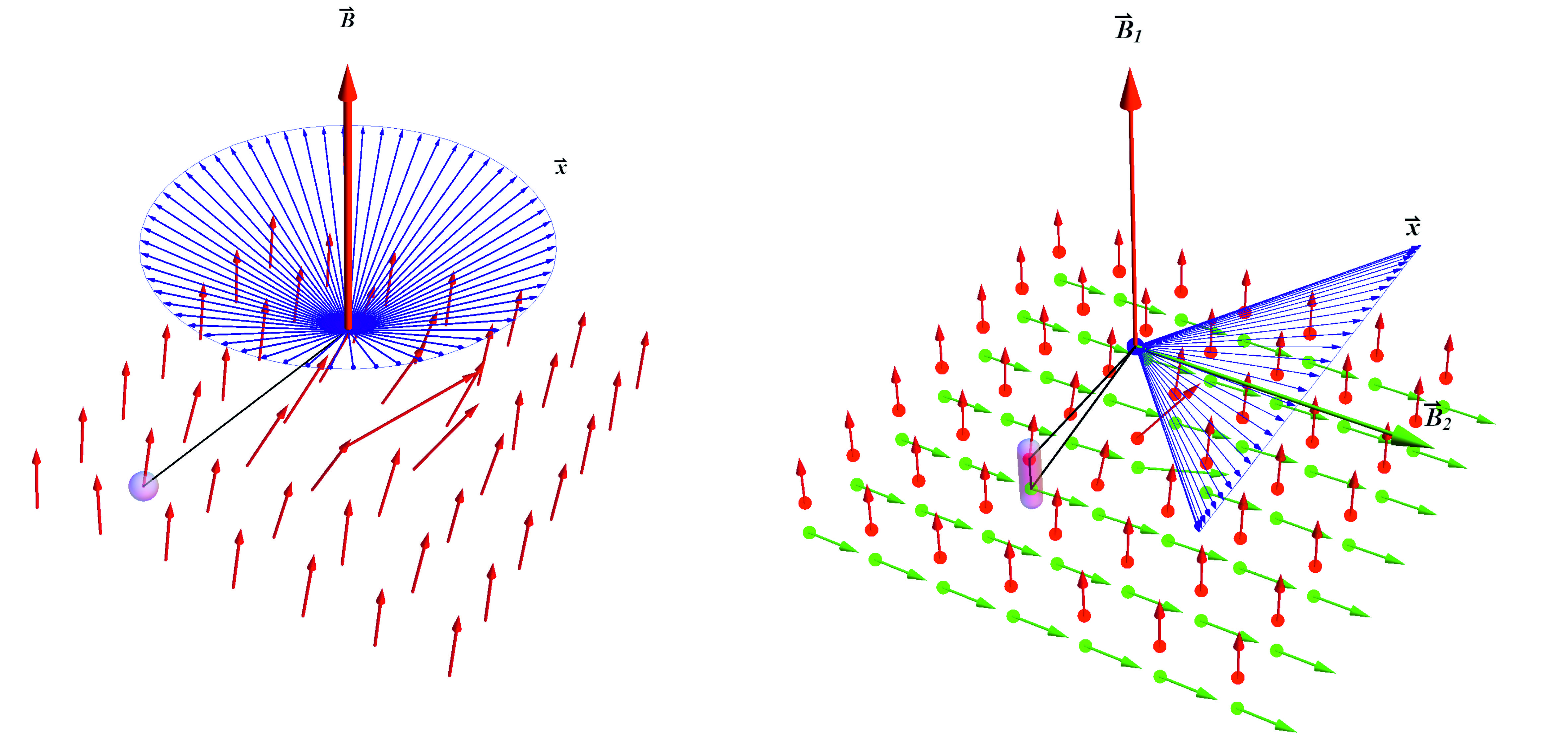
Dynamics of the generalized spin as generated by its interaction with
a single coherent (macroscopic) state in three-dimensional space (left) or with a pair of coherent states in four-dimensional space (right) [DB16].
Quantum Theory and the Dimensionality of Physical Space
One of the oldest questions in physics—why is space three-dimensional?—has resurfaced in the context of operational reconstructions. Despite the exponentially large Hilbert space dimension of composite quantum systems, experimental data is organized and interpreted within a three-dimensional spatial framework. What determines this dimensionality?
We explored this question by distinguishing between two kinds of dimensionality:
- The state space dimension of elementary systems
- The geometrical dimension of physical space
By requiring dynamical consistency between microscopic quantum systems and macroscopic transformation devices (e.g., laboratory apparatuses treated as classical limits of quantum systems), we found that this "closeness condition" constrains the two spaces to coincide in three dimensions [DB16]. This result suggests that the observed dimensionality of space may follow from the internal consistency of quantum theory when extended to macroscopic systems.
References
[OR1] N. M. Sanchez & B. Dakić, Reconstruction of Quantum Particle Statistics: Bosons, Fermions, and Transtatistics, Quantum 8, 1473 (2024)
[DB09] B. Dakić & Č. Brukner, Quantum Theory and Beyond: Is Entanglement Special?, arXiv:0911.0695
[DB16] B. Dakić & Č. Brukner, The Classical Limit and Dimensionality of Space, arXiv:1307.3984
[Har01] L. Hardy, Quantum Theory from Five Reasonable Axioms, arXiv:quant-ph/0101012
