Operational reconstruction of quantum theory
The origin of Hilbert space
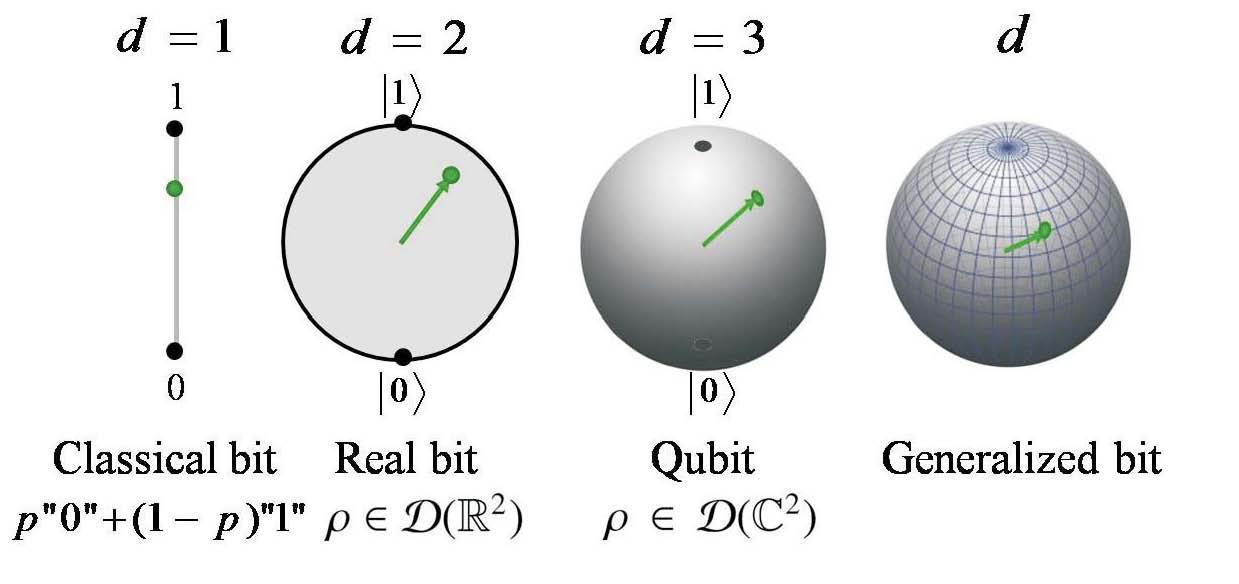
State spaces of a two-dimensional system in the generalized
probabilistic theories [DB09].
The origin of Hilbert space
It is often said that the birth of quantum information was inspired by research into the foundational problems of quantum physics. Many quantum information protocols and tasks are deeply rooted in foundational thinking. In recent years we are experiencing an opposite trend. Namely, thinking about practical problems leads us to novel insights and conceptual understanding of abstract formalism in quantum theory. This bottom-up approach aims to identify simple operational principles from which the formalism of quantum theory can be recovered—so-called reconstruction of quantum theory (see [Har16] for a historic account of the development of the field).
The field of operational reconstructions started in 2001, with the pioneering work of Hardy [Har01]. He introduced a whole hierarchy of “reasonable” probabilistic theories, among which quantum mechanics was uniquely identified on the basis of the simplicity axiom (quantum is the simplest theory compatible with the other axioms). Nevertheless, the simplicity axiom was rather ad hoc, and did not have a physical justification. This was considered as a serious open problem, and for many years there was not much progress towards its resolution. In 2009, together with Č. Brukner we made a crucial step forward by showing that quantum theory can be determined solely on physical principles, i.e. as a junction of three information-theoretic assumptions [DB09]: 1) the principle of limited information content, 2) the existence of continual reversible dynamics, and 3) tomographic locality. Our work re-opened the field (see the media coverage in New Scientist: R. Webb, Is quantum theory weird enough for the real world?, in 2010) and it was followed by a sequence of new reconstructions [CAP11, MM11, DB16, HW17].
Although, one could say that the present status of operational reconstructions is quite satisfactory, we are still missing a complete coherent picture. What follows from several reconstructions [Har01, DB09, MM11] is that quantum theory seems to be a unique combination of two postulates only: reversible dynamics and probability theory [DM17]. The affirmative answer to this conjecture will certainly give a clearer picture of the foundations of physical theories in general. For example, we can argue that classical physics combines in a unique way reversibility and determinism, whereas quantum theory is the unique combination of reversibility and indeterminism (as quantified by probabilities).
The dimensionality of space
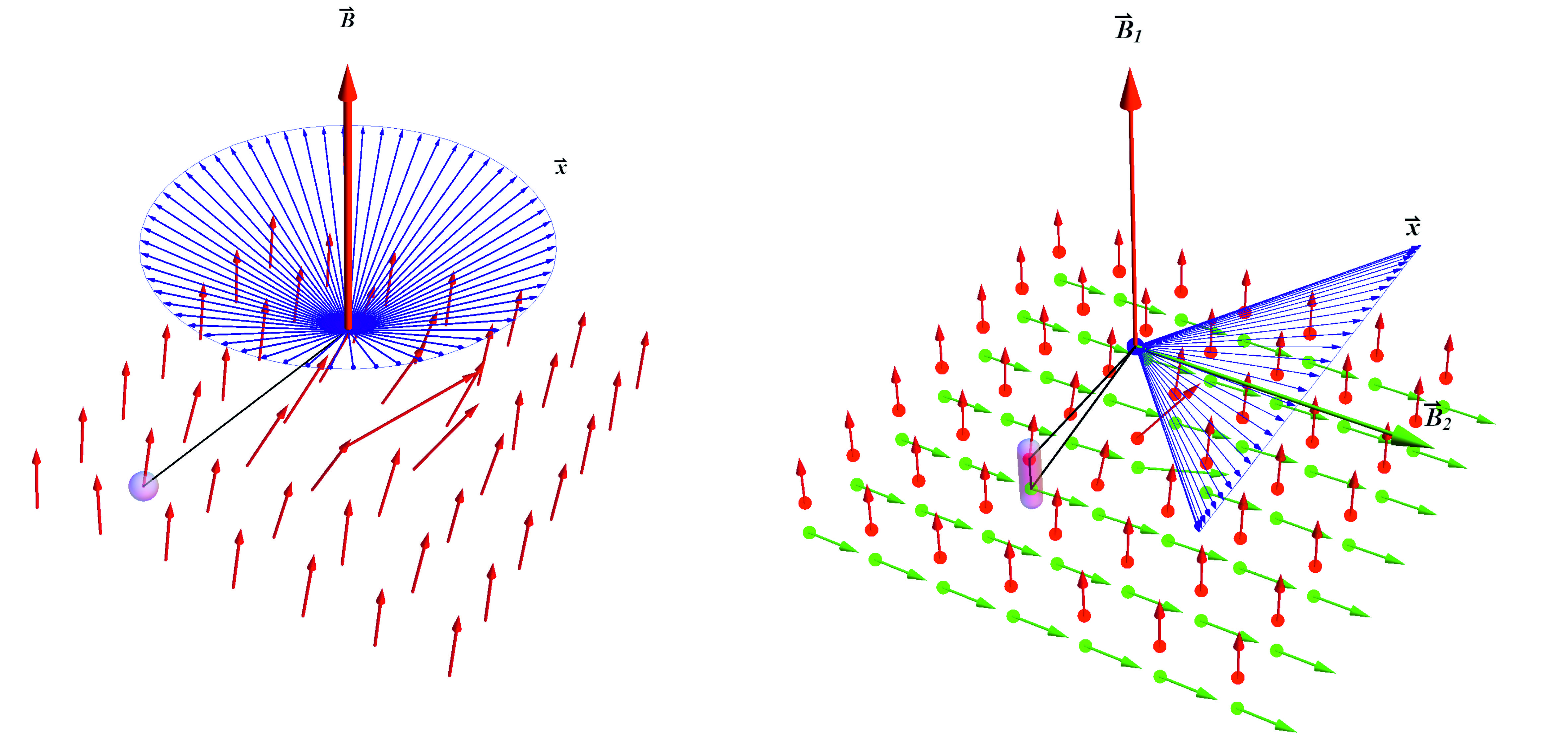
Dynamics of the generalized spin as generated by its interaction with
a single coherent (macroscopic) state in three-dimensional space (left) or with a pair of coherent states in four-dimensional space (right) [DB16].
The dimensionality of space
Why is space three dimensional? Although the quantum state space dimension (dimension of Hilbert space) for a macroscopic object is exponentially large (in the number of the object’s constituents), we still find ourselves organizing data in a three-dimensional space. Why does this discrepancy persist? Can there be more dimensions? We have been studying this question within an operational framework applied to a physical theory [DB16]. Here one distinguishes two spaces, the state space of “elementary systems” and the physical space in which “laboratory devices” are embedded. Each of those spaces has its own dimension: the minimal number of real parameters (coordinates) needed to specify the state of the system or a point within the physical space. The two dimensions coincide in a natural way under the following closeness requirement: the dynamics of a single elementary system can be generated by the invariant interaction between the system and a “macroscopic transformation device” that is itself described within the theory in the macroscopic (classical) limit. We have shown that the closeness assumption can be used to distinguish quantum theory from other theories in a unique way (see the media coverage in New Scientist: M. Chalmers, “Why space has exactly three dimensions”, in 2013). In our work, we focused on the rotational degree of freedom (i.e. spin). In the future, we want to apply our techniques for the translational degrees of freedom, and to incorporate full non-relativistic symmetries (Galilei group). Finally, we plan to study relativistic symmetries of elementary quantum systems (Poincare group) and their relation to the structure of classical (relativistic) spacetime.
References
[Har01] L. Hardy, Quantum theory from five reasonable axioms. arXiv:quant-ph/0101012 (2001).
[Har16] L. Hardy, Reconstructing quantum theory, in “Quantum Theory: Informational Foundations and Foils” eds. G. Chiribella and R. Spekkens, Springer 2016.
[DB09] B. Dakić and Č. Brukner, Quantum Theory and Beyond: Is Entanglement Special?, In Deep beauty, Ed Halvorson, H. (Cambridge Press, 2011), arXiv:0911.0695 (2009).
[CAP11] G. Chiribella, G. M. D’Ariano, and P. Perinotti, Informational derivation of quantum theory, Phys. Rev. A 84, 012311 (2011).
[MM11] L. Masanes and M. Müller, A derivation of quantum theory from physical requirements. New J. Phys. 13, 063001 (2011).
[DB16] B. Dakić and Č. Brukner, The classical limit of a physical theory and the dimensionality of space. In Quantum Theory: Informational Foundations and Foils, Eds. Chiribella, G. & Spekkens, R. (Springer, 2016), arXiv:1307.3984.
[HW17] P. A. Höhn and C. S. P. Wever, Quantum theory from questions. Phys. Rev. A, 95 (012102), 2017.
[DM17] See Open quantum problems, Problem 42: Reversible dynamics on composite systems, oqp.iqoqi.univie.ac.at.
