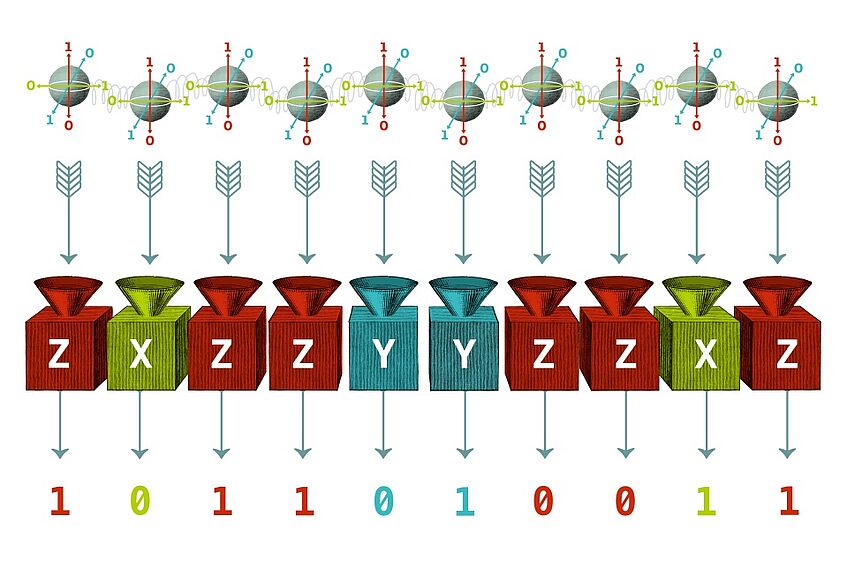
As engineered quantum systems advance, the ability to generate increasingly large quantum states has experienced rapid development. In this context, verifying large entangled systems represents one of the main challenges in employing such systems for reliable quantum information processing. Though the most complete technique is undoubtedly full tomography, the inherent exponential increase of experimental and post-processing resources with system size makes this approach infeasible at even moderate scales. Other methods aiming at probing only specific properties of the system, such as entanglement detection via witness operators, generally demand much less effort but still consume large numbers of copies for reliable estimates, which may go beyond the reach of the large-scale regime. For this reason, there is currently an urgent need to develop novel techniques that surpass these limitations. In our research group, we develop novel techniques [VQ1-VQ5] focusing on such scenarios with a limited and fixed number of resources and thus prove suitable for systems of arbitrary dimension. By adopting probabilistic frameworks [VQ5], we have pioneered novel verification methods in entanglement detection [VQ1, VC2], quantum state verification and certification [VQ3], and quantum state tomography [VQ4]. These hyper-efficient techniques define a dimension demarcation for partial tomography and open a path for novel applications in the burgeoning era of quantum technology.